1. F1 Score란?
F1 Score는 정밀도와 재현율을 결합한 지표이다.
정밀도와 재현율이 어느 한쪽으로 치우치치 않는 않을 때 상대적으로 높은 값을 가진다.
F1 Score의 공식은 아래와 같다.
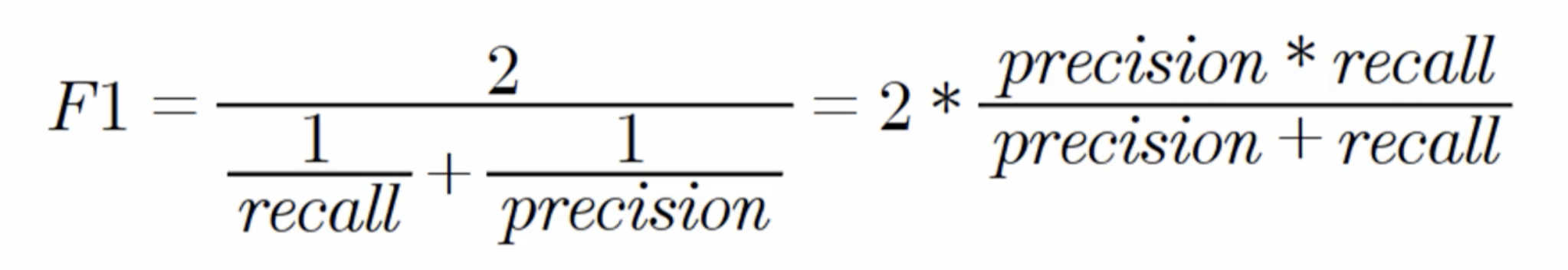
F1 Score가 높을수록 더 좋은 모델이라고 판단할 수 있는 기준이 된다.
아래의 예시를 살펴보자
A 예측 모델과 B예측 모델이 있다. A 예측 모델의 정밀도는 0.9, 재현율은 0.1로 차이가 많이 나고 B 예측 모델은 정밀도가 0.5, 재현율은 0.5로 정밀도와 재현율이 큰 차이가 없다.
이 두 모델의 F1 Score을 계산해보면 A 예측 모델은 0.18, B 예측 모델은 0.5로 B 예측 모델이 더 우수한 F1 Score을 가지게 된다.
사이킷런에서는 F1 Score 계산을 위한 f1_score() 메소드를 지원한다.
f1_score 메소드를 간단하게 살펴보면 다음과 같다

2. ROC 곡선과 AUC
ROC 곡선이란 FPR(False Positive Rate)가 변할 때 TPR(True Positive Rate)가 어떻게 변하는지 나타내는 곡선이다.
- TPR은 재현율로서 민감도라도 부른다.
- FPR은 실제는 Negative인데 Postive로 잘못 예측한 비율로 공식은 다음과 같다.
FPR = FP / (FP+TN) - 임계값을 1로 하면 FPR은 0이되고 0으로하면 FPR은 1이된다.
(임계값이 1에 가까울수록 재현율은 0에 가까워지고 이에 따라 FPR 역시 0에 가까워지게된다) - 임계값이 높아질 수록 TPR이 천천히 감소하는 모델이 좋은 모델이다.
FPR을 X축으로, TPR을 Y축으로 놓고 변화를 살펴보면 아래와 같이 곡선 형태로 나타나게 된다.
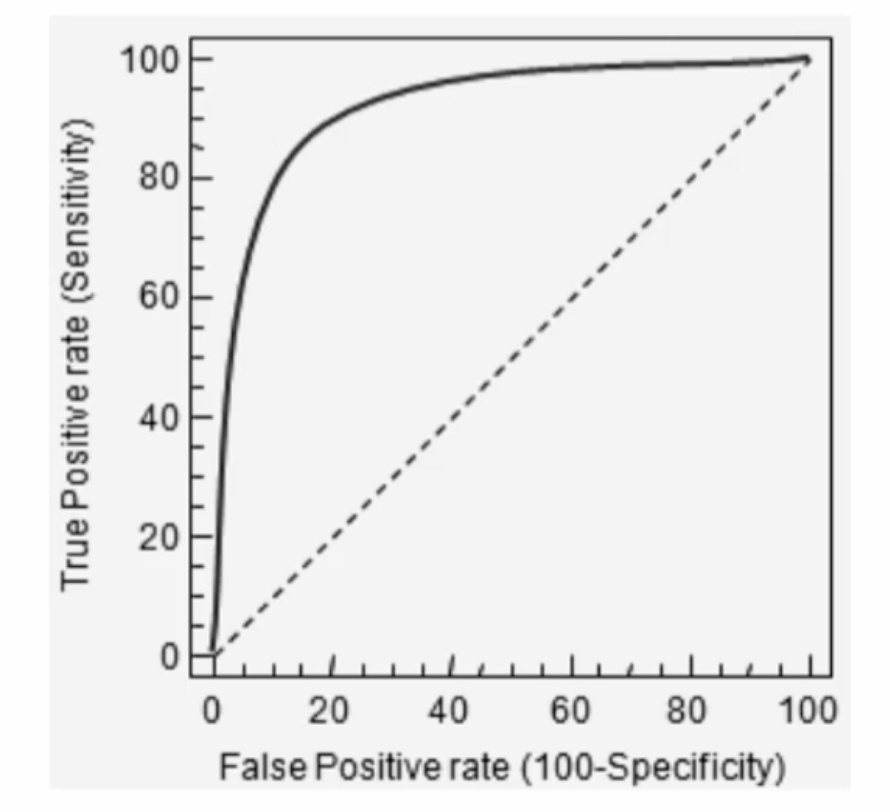
AUC(Area Under Curve) 값은 ROC 곡선 및의 면적을 구한 것이다.
일반적으로 의학분야에서 많이 사용되지만, 머신러닝의 인진 분류 모델의 예측 성능을 판단하는 중요한 평가 지표이다.
일반적으로 1에 가까울수록 좋은 수치이다.
사이킷런에서는 ROC 곡선을 계산하기 위한 roc_curve() 메소드를 지원하고 이를 통해 TPR, FPR 값을 구할 수 있다.
roc_curve() 메소드를 간단하게 살펴보면 다음과 같다.

3. F1 Score, ROC 곡선과 AUC 실습
F1 Score와 Roc곡선, AUC 실습을 위해 앞 포스팅에서 진행했던 오차행렬(오차행렬(Confusion Matrix), 정밀도(Precision), 재현율(Recall))에서 실습한 코드를 바탕으로 실습해보자.
간단히 설명하면 타이타닉 데이터를 기반으로 Null처리, 불필요 피처 제거, 레이블 인코딩을 수행한다.
import numpy as np
import pandas as pd
import warnings
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
warnings.filterwarnings('ignore')
import pandas as pd
from sklearn.preprocessing import LabelEncoder
# Null 처리 함수
def fillna(df):
df['Age'].fillna(df['Age'].mean(),inplace=True)
df['Cabin'].fillna('N',inplace=True)
df['Embarked'].fillna('N',inplace=True)
df['Fare'].fillna(0,inplace=True)
return df
# 머신러닝 알고리즘에 불필요한 피처 제거
def drop_features(df):
df.drop(['PassengerId','Name','Ticket'],axis=1,inplace=True)
return df
# 레이블 인코딩 수행.
def format_features(df):
df['Cabin'] = df['Cabin'].str[:1]
features = ['Cabin','Sex','Embarked']
for feature in features:
le = LabelEncoder()
le = le.fit(df[feature])
df[feature] = le.transform(df[feature])
return df
# 앞에서 설정한 Data Preprocessing 함수 호출
def transform_features(df):
df = fillna(df)
df = drop_features(df)
df = format_features(df)
return df
# 원본 데이터를 재로딩, 데이터 가공, 학습데이터/테스트 데이터 분할.
titanic_df = pd.read_csv('./titanic_train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df= titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)
X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, \
test_size=0.20, random_state=11)
lr_clf = LogisticRegression(solver='liblinear')
lr_clf.fit(X_train , y_train)
pred = lr_clf.predict(X_test)
이제 사이킷런에서 제공하는 f1_score() 함수를 이용하여 F1_Score값을 구해보자.
from sklearn.metrics import f1_score
f1 = f1_score(y_test , pred)
print('F1 스코어: {0:.4f}'.format(f1))▶ Out
F1 스코어: 0.7966
이제 임계값에 변화에 따른 F1 Score값의 변화를 살펴보자.
이전 포스팅에서 진행했던 Binarizer를 이용하여 임계값을 적용하고 임계값이 변함에 따라 오차행렬, 정밀도, 재현율, F1 Score 값을 출력해본다. 임계값이 변함에 따라 정밀도와 재현율이 변화하고 그에 따라 F1 Score가 변화하는 것을 확인할 수 있다.
from sklearn.preprocessing import Binarizer
from sklearn.metrics import accuracy_score, precision_score , recall_score
def get_eval_by_threshold(y_test , pred_proba_c1, thresholds):
# thresholds list객체내의 값을 차례로 iteration하면서 Evaluation 수행.
for custom_threshold in thresholds:
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1)
custom_predict = binarizer.transform(pred_proba_c1)
print('임곗값:',custom_threshold)
get_clf_eval(y_test , custom_predict)
print('--------------------------------------------------')
def get_clf_eval(y_test , pred):
confusion = confusion_matrix( y_test, pred)
accuracy = accuracy_score(y_test , pred)
precision = precision_score(y_test , pred)
recall = recall_score(y_test , pred)
# F1 스코어 추가
f1 = f1_score(y_test,pred)
print('오차 행렬')
print(confusion)
# f1 score print 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}, F1:{3:.4f}'.format(accuracy, precision, recall, f1))
thresholds = [0.4 , 0.45 , 0.50 , 0.55 , 0.60]
pred_proba = lr_clf.predict_proba(X_test)
get_eval_by_threshold(y_test, pred_proba[:,1].reshape(-1,1), thresholds)▶ Out
임곗값: 0.4
오차 행렬
[[97 21]
[11 50]]
정확도: 0.8212, 정밀도: 0.7042, 재현율: 0.8197, F1:0.7576
--------------------------------------------------
임곗값: 0.45
오차 행렬
[[105 13]
[ 13 48]]
정확도: 0.8547, 정밀도: 0.7869, 재현율: 0.7869, F1:0.7869
--------------------------------------------------
임곗값: 0.5
오차 행렬
[[108 10]
[ 14 47]]
정확도: 0.8659, 정밀도: 0.8246, 재현율: 0.7705, F1:0.7966
--------------------------------------------------
임곗값: 0.55
오차 행렬
[[111 7]
[ 16 45]]
정확도: 0.8715, 정밀도: 0.8654, 재현율: 0.7377, F1:0.7965
--------------------------------------------------
임곗값: 0.6
오차 행렬
[[113 5]
[ 17 44]]
정확도: 0.8771, 정밀도: 0.8980, 재현율: 0.7213, F1:0.8000
--------------------------------------------------
이번에는 ROC 곡선과 AUC 값을 구해보자.
ROC 곡선을 위해 Positive일 때의 예측확률을 추출해준다. 그리고 실제 타겟값과 예측값을 roc_curve에 파라미터로 넣어준다.
그리고 임계값을 5개 단계로 추출하고 임계값이 증가함에 따라 FPR, TPR도 증가하는 것을 확인할 수 있다.
from sklearn.metrics import roc_curve
# 레이블 값이 1일때의 예측 확률을 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
fprs , tprs , thresholds = roc_curve(y_test, pred_proba_class1)
# 반환된 임곗값 배열에서 샘플로 데이터를 추출하되, 임곗값을 5 Step으로 추출.
# thresholds[0]은 max(예측확률)+1로 임의 설정됨. 이를 제외하기 위해 np.arange는 1부터 시작
thr_index = np.arange(1, thresholds.shape[0], 5)
print('샘플 추출을 위한 임곗값 배열의 index:', thr_index)
print('샘플 index로 추출한 임곗값: ', np.round(thresholds[thr_index], 2))
# 5 step 단위로 추출된 임계값에 따른 FPR, TPR 값
print('샘플 임곗값별 FPR: ', np.round(fprs[thr_index], 3))
print('샘플 임곗값별 TPR: ', np.round(tprs[thr_index], 3))▶ Out
샘플 추출을 위한 임곗값 배열의 index: [ 1 6 11 16 21 26 31 36 41 46]
샘플 index로 추출한 임곗값: [0.94 0.73 0.62 0.52 0.44 0.28 0.15 0.14 0.13 0.12]
샘플 임곗값별 FPR: [0. 0.008 0.025 0.076 0.127 0.254 0.576 0.61 0.746 0.847]
샘플 임곗값별 TPR: [0.016 0.492 0.705 0.738 0.803 0.885 0.902 0.951 0.967 1. ]
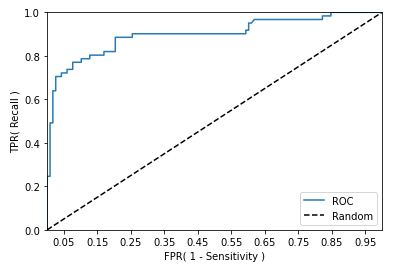
그리고 ROC 곡선을 그래프로 그려보면 다음과 같다.
def roc_curve_plot(y_test , pred_proba_c1):
# 임곗값에 따른 FPR, TPR 값을 반환 받음.
fprs , tprs , thresholds = roc_curve(y_test ,pred_proba_c1)
# ROC Curve를 plot 곡선으로 그림.
plt.plot(fprs , tprs, label='ROC')
# 가운데 대각선 직선을 그림.
plt.plot([0, 1], [0, 1], 'k--', label='Random')
# FPR X 축의 Scale을 0.1 단위로 변경, X,Y 축명 설정등
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
plt.xlim(0,1); plt.ylim(0,1)
plt.xlabel('FPR( 1 - Sensitivity )'); plt.ylabel('TPR( Recall )')
plt.legend()
plt.show()
roc_curve_plot(y_test, lr_clf.predict_proba(X_test)[:, 1] )▶ Out
'ML > 평가(Evaluation)' 카테고리의 다른 글
| 피마 인디언 당뇨병 데이터로 머신러닝 평가하기 (0) | 2024.03.25 |
|---|---|
| 오차행렬(Confusion Matrix), 정밀도(Precision), 재현율(Recall) (2) | 2024.03.11 |
| 정확도(Accuracy)란? (0) | 2024.02.21 |